5.2 统一货币

发表于 | 更新于 | 分类于 | 阅读次数：

实验任务

\(C\)国家有\(N\)个城市，用\(N-1\)条道路连接，保证任意两个城市连通，整个国家中由两种流通的货币，有的城市使用货币\(A\)币，有的城市用货币\(B\)币，现国王希望统一货币，便于管理。现在只有一种操作：

\(change(v)\)，\(v\)表示国家中的某个城市，该操作可以改变所有城市\(U=\lbrace u|u\)到\(v\)的最短路径上的城市当前所使用的货币都与\(v\)相同\(\rbrace\)的货币类型，如果是\(A\)则变成\(B\)，是\(B\)则变成\(A\)。请问最少需要几次操作，能使整个国家货币统一。

数据输入

第一行包括一个整数\(N(1\leq N\leq 20000)\)，表示城市个数。 第二行为\(N\)个整数\(t_i\)，表示城市的货币类型。\(t_i=0\)表示第\(i\)个城市使用\(A\)货币，\(t_i=1\)表示第\(i\)个城市\(B\)货币类型。然后输入\(N-1\)行，每行包括两个整数\(v_i\)，\(u_i\ (1\leq v_i,u_i\leq N)\)，表示城市\(v_i\)和城市\(u_i\)之间有一条道路。

数据输出

输出一个个数 K，表示需要使用的最小操作数。

输入示例 输出示例
2
0 1 1 0 0 0 1
1 2
1 3
2 4
2 5
3 6
3 7		 2

提示

\(change(3)\)：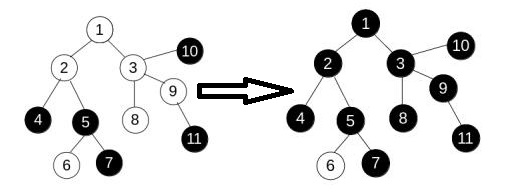

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <stdio.h>
#include <vector>
#include <string.h>
using namespace std;
#define maxn 20005

class Node{
public:
    int type;
    vector<int> son;
    Node(){}
};

class Tree{
public:
    Node node[maxn];
    void in(){
        int n, i, u, v;
        scanf("%d", &n);
        for (i = 1; i <= n; ++i){
            scanf("%d", &node[i]);
        }
        for (i = 1; i < n; ++i){
            scanf("%d%d", &u, &v);
            node[u].son.push_back(v);
            node[v].son.push_back(u);
        }
    }
    //parent:fa <-> root <-> son，判断是否处理过了！
    int bfs(int root, int &leaf, int deep, int parent){
        leaf = root;
        int ret = deep;
        for (int i = 0; i < node[root].son.size(); ++i){
            int son = node[root].son[i];
            int leaft = root;
            if (son != parent){
                int deept = node[root].type == node[son].type ? deep : deep + 1;
                int len = bfs(son, leaft, deept, root);
                if (len > ret){
                    ret = len;
                    leaf = leaft;
                }
            }
        }
        return ret;
    }
}tree;

int main(){
    tree.in();
    int leaf = 1;
    //树的直径算法
    tree.bfs(1, leaf, 1, 0);
    int len = tree.bfs(leaf, leaf, 1, 0);
    printf("%d\n", len >> 1);
    return 0;
}

设计思路与复杂度分析

压缩点：根据操作的特征，容易发现，所有点权相同且互相“联通”的点，操作一致。可以考虑将它们压缩成一个点，缩完点之后得到的是一棵黑白相间的树。

考虑一种操作方式：选一个点，从头到尾一直翻转它。对于这样的操作方式，树高决定操作次数。因此，为了让操作次数最少，需要选择一个点，使得树高最小，而这个点称之为树的中心。寻找树的中心方法是：找出树中距离最远的两个点，以这两个点为端点的路径，称之为树的直径，直径中间的那个点就是树的中心。于是题目等价于求出树直径长度Len，最终的答案为\(floor(Len/2)\)。

贪心证明：为何一直翻转树的中心会是最优策略？若每次翻转直径的非叶子结点，缩点之后，结点数减少2。若每次翻转直径的叶子结点，缩点之后，结点数减少1。所以显然优先翻转非叶子结点。要将直径全部变成一种颜色，至少需进行Len/2次操作，结果不会优于一直翻转树的中心策略。

树的直径：（证明有兴趣可以翻翻算法导论）对于树的任意一个结点a，找到距离结点a的最远结点A；找到距离结点A的最远结点B，则A和B所在的路径就是树的直径。

复杂度分析：压缩点可以考虑重新建树时间为\(T1(n)=n\)，但是其实么必要，在找树的直径的时候对于同色的子节点深度不增加即可达到目的。找树的直径时间为\(T2(n)=2\times n\)。所以总时间复杂度为\(T(n)=2\times n=O(n)\)。

0%