5.1 综合实力

发表于 | 更新于 | 分类于 | 阅读次数：

实验任务

大陆上有\(N\)个国家，用\(N-1\)条道路连接，保证任意两个国家之间有路径可达。弱肉强食，国家之间的战争随时会爆发，因此国家与国家之间选择结盟避免被吞并。因为每个国家的综合实力\(A\)不一样，只要联盟的综合实力总和相等，就能保证陆地上暂时的和平。现在需要破坏 2 条道路，将这\(N\)个国家划分成 3 个联盟，使各个联盟国家综合实力总和相等。

数据输入

输入第一行为整数\(N(3\leq N\leq 20000)\)，表示国家的个数。接下来\(N\)行，包括两个整数\(T\)和\(A\ (1\leq A\leq 100)\)，第\(i\)行表示第\(i\)条道路，连接国家\(i\)和国家\(T\)（\(T=0\)表示这条道路不存在），且国家\(i\)的综合实力为\(A\)。国家编号从 1 到\(N\)，所有的道路都是双向的。

数据输出

如果没有解决方案则输出-1。否则输出两个整数，表示这两条道路的编号（即在输入中第几个给出，编号从 1 开始），按从小到大的顺序输出。

输入示例 输出示例
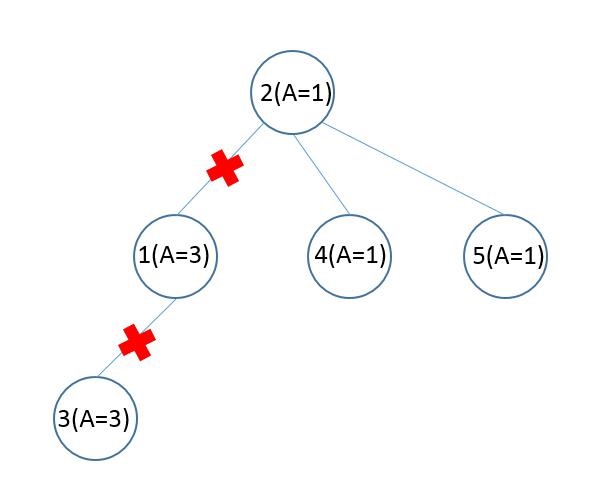
5
2 3
0 1
1 3
2 1
2 1		 1 3

提示

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <stdio.h>
#include <vector>
#include <algorithm>
using namespace std;
#define maxn 20005

class Node{
public:
    int power;
    vector<int> son;
    Node() :power(0){ son.clear(); }
};

class Tree{
public:
    int total;
    Node node[maxn];
    void in(const int & n){
        int parent;
        for (int i = 1; i <= n; ++i){//0是虚节点，其子节点存储根节点的编号
            scanf("%d%d", &parent, &node[i].power);
            node[parent].son.push_back(i);//下标只会出现一次，做son没问题
            total += node[i].power;
        }
    }
    bool solve(){
        if (total % 3) return false;//不为3的整数倍必定无解
        total /= 3;
        return dfs(node[0].son[0]);
    }
    bool dfs(int root){//dfs(后序遍历)，并将合法子树的根提升为虚节点的子树
        for (unsigned int i = 0; i < node[root].son.size(); ++i){
            if (!dfs(node[root].son[i]))return false;
            //剪枝：已找到两颗满足条件的子树，那么余下的节点一定满足条件
            if (node[0].son.size() == 3)return true;
            node[root].power += node[node[root].son[i]].power;
            if (node[root].power>total)return false;//剪枝：该子树无法凑齐1/3
        }
        if (node[root].power == total){
            node[0].son.push_back(root);
            node[root].power = 0;
        }
        return true;
    }
    Tree() :total(0){}
}tree;

int main(){
    int n;
    scanf("%d", &n);
    tree.in(n);
    if (!tree.solve()) { printf("-1\n"); }
    else{
        int ans1 = tree.node[0].son[1];
        int ans2 = tree.node[0].son[2];
        if (ans1>ans2)swap(ans1, ans2);
        printf("%d %d\n", ans1, ans2);
    }
    return 0;
}

设计思路与复杂度分析

设每一颗子树的综合实力为其所有子树的实力与根的实力之和，则对于某一棵子树，若其综合实力刚好等于\(1/3\)根树的综合实力，那么将该子树与父节点切断联系独立成一棵树即可。实现上只需要\(dfs\)（后序遍历）即可得到每一颗子树的综合实力。 在\(dfs\)的时候分如下3情况可优化：

  1. 某一颗树其所有子树都未达到\(1/3\)，但是与其结合之后超过1/3，那么无解，直接返回\(false\)；
  2. 若找到两颗子树分别满足\(1/3\)，那么在预判总量为3的倍数的前提下剩余节点一定满足条件，可直接返回\(true\)；
  3. 找到符合条件的子树的时候直接将其根设为虚节点的儿子，则无需再次遍历查找答案。

如此所有时间耗费为输入数据和\(dfs\)的时间，复杂度为：\(O(n)\)。

0%