6.3 生日Party

发表于 | 更新于 | 分类于 | 阅读次数：

实验任务

在 11 月 11 日生日的小\(X\)同学刚刚过完了他的生日，朋友们在他家开心地举办了盛大的 party 为他庆生。

Party 结束后，留下了\(n\)瓶未喝完的饮料，第\(i\)瓶饮料的容积为\(b_i\)，剩余饮料体积为\(a_i\)。小\(X\)同学十分喜欢这种饮料，希望把剩下的饮料都整理起来慢慢喝，但是家里的冰箱太小了，没有足够多的位置放瓶子，所以他希望用最少的瓶子装完所有剩下的饮料（饮料的体积不超过瓶子的容积）。同时，从一个瓶子倒体积\(v\)的饮料到另一个瓶子需要花费\(v\)单位的时间，小\(X\)急着去看电视剧，他想知道在使用最少瓶子的前提下，最少需要花费多少单位时间能把所有饮料倒到这些瓶子里？

数据输入

输入的第一行为包括一个整数\(n\ (1\leq n\leq 100)\)表示剩余饮料的瓶数。接下来一行，\(n\)个整数\(a_i\ (1\leq a_i\leq 100)\)表示\(n\)瓶饮料所剩体积。最后一行，\(n\)个整数\(b_i\ (1\leq b_i\leq 100)\)表示\(n\)瓶饮料瓶子容积。

数据输出

输出两个整数分别表示所需的最少瓶子数和倒饮料所需最少时间。

输入示例 输出示例
4
3 3 4 3
4 7 6 5		 2 6
2
1 1
100 100		 1 1

源代码（分支限界法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;

#define maxn 105

inline int max(int a, int b){ return a > b ? a : b; }

struct Node {
    int a, b;
    bool operator < (const Node& x) const {
        return b<x.b;
    }
} ns[maxn];

struct Heap {
    int cur, val, vol, cnt, up;
    Heap(int cur, int val, int vol, int cnt, int up)
        :cur(cur), val(val), vol(vol), cnt(cnt), up(up) {}
    bool operator < (const Heap& hp) const {
        return up<hp.up || up == hp.up&&cnt<hp.cnt;
    }
    Heap() {}
};

int n;
int sumv[maxn], dp[maxn][maxn];

int main() {
    int i, j, suma = 0, sumb = 0;
    scanf("%d", &n);
    for (i = 1; i <= n; ++i) {
        scanf("%d", &ns[i].a);
        suma += ns[i].a;
    }
    for (i = 1; i <= n; i++) scanf("%d", &ns[i].b);
    sort(ns + 1, ns + n + 1);
    for (i = n; i >= 1 && suma>sumb; --i) {
        sumb += ns[i].b;
    }
    //k代表最少瓶数
    int k = n - i;
    sumv[0] = 0;
    for (i = 1; i <= n; i++) sumv[i] = sumv[i - 1] + ns[i].b;
    memset(dp, -1, sizeof(dp));
    for (i = 0; i <= n; i++) {
        dp[i][0] = 0;
        for (j = 1; j <= i; j++) {
            dp[i][j] = max(dp[i - 1][j - 1] + ns[i].a, dp[i - 1][j]);
        }
    }
    int res = 0;
    priority_queue<Heap> pq;
    pq.push(Heap(n, 0, 0, 0, dp[n][k]));
    while (!pq.empty()) {
        Heap u = pq.top();
        pq.pop();
        if (u.cnt == k){
            res = u.up;
            break;
        }
        //没儿子
        int cur_vol = u.vol + sumv[u.cur] - sumv[u.cur - (k - u.cnt)];
        int lef_cnt = k - u.cnt;
        if (cur_vol<suma || lef_cnt>u.cur || u.cur <= 0) continue;
        //左子树
        Heap lson = Heap(u.cur - 1, u.val + ns[u.cur].a,
            u.vol + ns[u.cur].b, u.cnt + 1,
            u.val + ns[u.cur].a + dp[u.cur - 1][k - 1 - u.cnt]);
        pq.push(lson);
        //右子树，一个小条件提前判断一下
        if (u.cur - 1 >= k - u.cnt){
            Heap rson = Heap(u.cur - 1, u.val, u.vol,
                u.cnt, u.val + dp[u.cur - 1][k - u.cnt]);
            pq.push(rson);
        }
    }
    printf("%d %d\n", k, suma - res);
    return 0;
}

设计思路与复杂度分析

题目要求用最少瓶子的前提下耗时也最少。首先确定需要瓶子个数\(k\)，那么问题转化为用\(k\)个瓶子装所有饮料，且转移耗时最少。等价为如下的优化问题： 考虑分支限界法求最大值问题，上界定义为：\(upper\_bound=cura+h(k-curk)\)，其中\(cura\)表示已经选取的瓶子的饮料体积；\(curk\)表示已经选取的瓶子数，\((k-curk)\)表示还要选的瓶子个数；\(h(k-curk)\) 表示从剩余的瓶子中取出\(k-curk\)个瓶子的最大饮料体积。有如下剪枝策略：

预处理阶：按照瓶子体积升序排列以求得\(k\)且方便剪枝。然后用运行一次动态规划算法计算\(dp(i,j)\)，表示前\(i\)个瓶子中，选\(j\)个瓶子，能得到的最大饮料体积为计算\(upper\_bound\)做准备。

优先队列实现分值限界法：从第n个瓶子开始搜，搜到第1个瓶子为止。每次找\(upper\_bound\)值最大的节点扩展。

下面是样例分析：

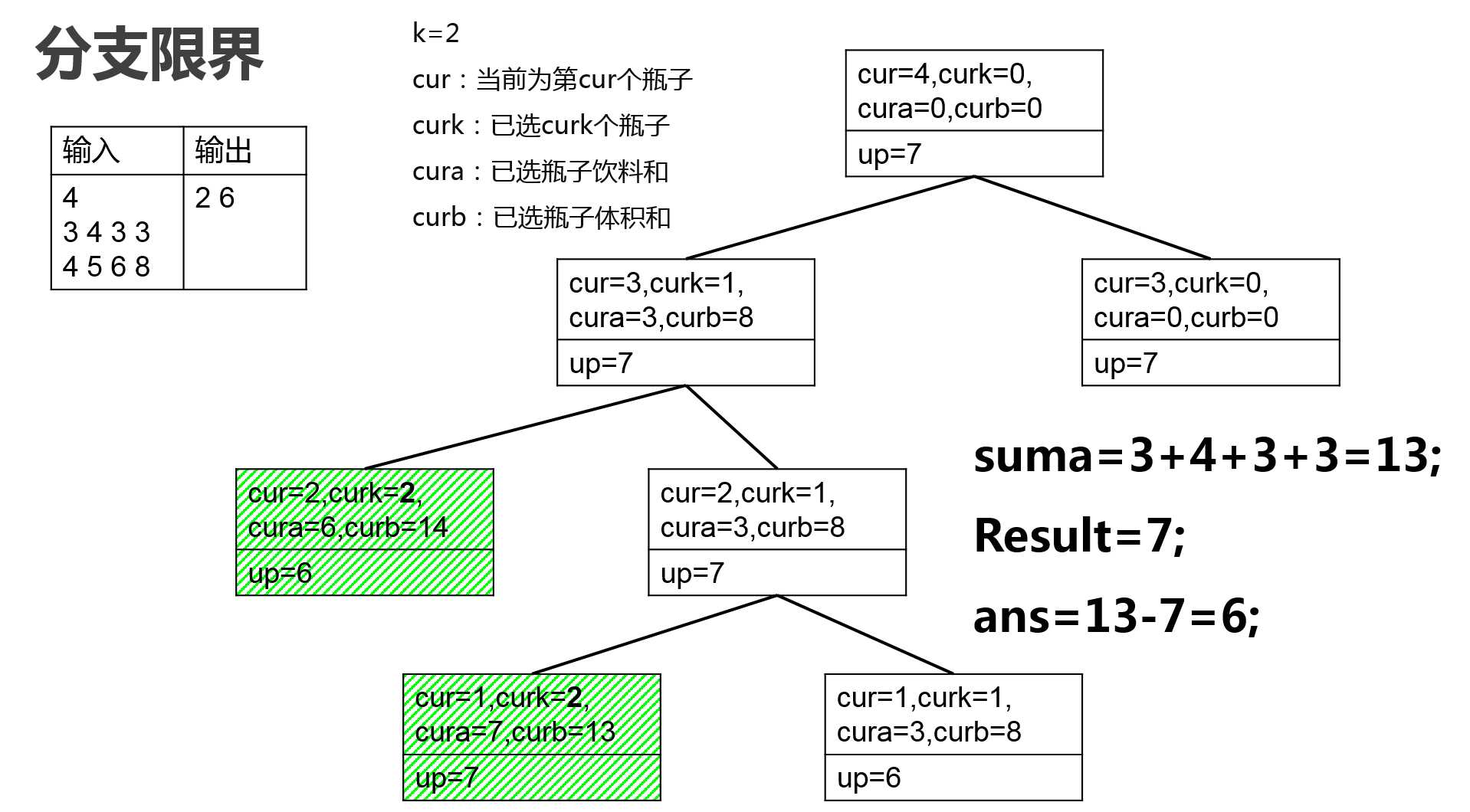
源代码（动态规划）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

inline int max(int a, int b){ return a < b ? b : a; }

struct bottle{
    int left, volume;
}bottles[105];

bool cmp(bottle a, bottle b){
    if (a.volume != b.volume)
        return a.volume>b.volume;
    else
        return a.left>b.left;
}
int dp[105][10005];

int main(){
    int n, i, j, k;
    scanf("%d", &n);
    int sum = 0;
    memset(dp, -1, sizeof(dp));
    for (i = 1; i <= n; i++)    {
        scanf("%d", &bottles[i].left);
        //所剩体积
        sum += bottles[i].left;
    }
    for (i = 1; i <= n; i++)
        scanf("%d", &bottles[i].volume);
    int cnt = 0;
    int total = 0;
    sort(bottles + 1, bottles + 1 + n, cmp);
    for (i = 1; i <= n; i++){//确定使用的最少的瓶子数
        total += bottles[i].volume;
        if (total >= sum){
            cnt = i;
            break;
        }
    }
    dp[0][0] = 0;
    for (i = 1; i <= n; i++){
        for (j = sum; (j - bottles[i].left) >= 0; j--){
            for (k = i; k >= 1; k--){
                //dp[i][j] 选i个瓶子其中自带j的水
                if (dp[k - 1][j - bottles[i].left] != -1)
                    dp[k][j] = max(dp[k][j], dp[k - 1][j - bottles[i].left] + bottles[i].volume);
            }
        }
    }
    int ans = 0;
    for (i = sum; i >= 1; i--){
        if (dp[cnt][i] >= sum){
            ans = sum - i;
            break;
        }
    }
    printf("%d %d\n", cnt, ans);
    return 0;
}

设计思路与复杂度分析

同分支限界法一样首先确定瓶子个数，但是无法使用前\(cnt\)容积大的瓶子来作为最后结果，因为有可能那\(cnt\)个瓶子外的瓶子剩余量很小且容积较大，或者\(cnt\)个瓶子内容积大却剩余少。选取的\(cnt\)个瓶子要尽量满足将剩余少的瓶子往剩余多的瓶子倒饮料，则找到\(cnt\)个瓶子并且他们剩余的饮料总量最大，则转移时间就最少。所以需要知道选\(cnt\)个瓶子时，可以装其他瓶子的剩余饮料总量可以是多少（\(cnt\)个瓶子的总容积-\(cnt\)个瓶子自己剩余的总饮料量）。如此得到状态转移方程： \[dp(i,j)=max(dp(i,j),dp(i-1,j-bottle_i.left)+bottle_i.volume)\] 其中\(dp(0,0)=0\)，\(dp(i,j)\)为选取\(i\)个瓶子且这\(i\)个瓶子自带\(j\)剩余总量的\(i\)个瓶子的最大总容积。

求解出上述转移方程后即可以通过方程 \[max(sum-init) \ s.t.\ dp[cnt][init] \geq sum,init = 1\cdots sum\] 最终获得所需时间是\(ans=sum-init\) 可以理解为求解cnt个瓶子并且自带剩余饮料总量最大。所需时间就是剩余饮料总量减去这\(cnt\)个瓶子自带的剩余总量。

0%