6.1 屠龙宝镜

发表于 | 更新于 | 分类于 | 阅读次数：

实验任务

小\(X\)同学最近沉迷页游——屠龙宝镜。游戏在一个\(N\times M\)的地图上进行，地图上有一些点设置有屠龙宝镜，玩家在地图的左上角，恶龙在地图的右下角。玩家在地图的左上角向右通过魔法发射一束能杀死恶龙的光线，光线通过地图直线传播，若玩家选择使用当前位置光线经过的宝镜，则宝镜会把光线朝上、下、 左、 右四个方向反射。但是每使用一个屠龙宝镜要消耗一定量的魔法值，魔法值的获取十分困难，因此小\(X\)同学希望利用最少的屠龙宝镜杀死恶龙。但是随着地图的增大，计算变得越来越困难，小\(X\)同学觉得游戏体验很差，你能帮帮他吗？

数据输入

输入的第一行为包括两个整数\(n,m\ (1\leq n, m\leq 1000)\)表示游戏地图的大小。接下来\(n\)行，每行包括\(m\)个字符用来表示地图。‘.’ 字符表示该地图位置为空地，‘#’ 字符表示该地图位置设置有屠龙宝镜。30%的数据\(n\times m\leq 30\)，70%的数据\(n\times m\leq 100\)，100%的数据\(n\times m\leq 1000\)。

数据输出

若能杀死恶龙，输出需要使用的最少屠龙宝镜，否则输出-1。

输入示例 输出示例
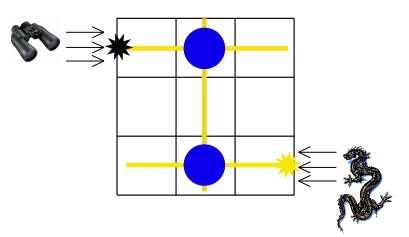
3 3
.#.
...
.#.		 2
4 4
##..
..#.
...#
...#		 -1

提示

# 源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <stdio.h>
#include <string.h>
#include <vector>
#include <queue>
using namespace std;

#define Inf 0x3f3f3f3f
#define maxn 1005

int cnt[maxn << 1];
bool flag[maxn << 1];
vector<int> tree[maxn << 1];

inline int min(int x, int y){ return x < y ? x : y; }

int bfs(int idx, int n){
    queue<int> myqueue;
    memset(cnt, Inf, sizeof(cnt));
    memset(flag, false, sizeof(flag));
    cnt[1] = 0;
    int i, father, son;
    myqueue.push(idx);
    while (!myqueue.empty()){
        father = myqueue.front();
        myqueue.pop();
        flag[father] = true;
        for (i = 0; i<tree[father].size(); i++){
            son = tree[father][i];
            if (!flag[son]){
                myqueue.push(son);
                cnt[son] = min(cnt[father] + 1, cnt[son]);
            }
        }
    }
    return cnt[n] == Inf ? -1 : cnt[n];
}

int main(){
    int n, m, i, j;
    scanf("%d%d\n", &n, &m);
    //行节点从1到n，列节点从n+1到n+m
    for (i = 1; i <= n; i++){
        for (j = 1; j <= m; j++){
            char c = getchar();
            if (c == '#'){
                tree[i].push_back(n + j);
                tree[n + j].push_back(i);
            }
        }
        getchar();
    }
    printf("%d\n", bfs(1, n));
    return 0;
}

设计思路与复杂度分析

可以把地图的每一行每一列看成是一个点，存在宝镜的地方就把它看成是某行的点到某列的边。这个时候就变成了从起点开始寻找到终点的最短路径。

建图：\(T_1(n)=O(n\times m)\)；搜索路径：\(T_2(n)=O(m+n)\)；综上所述，时间复杂度：\(T(n)=T_1+T_2=O(m\times n)\)。

0%