3.1 卡片游戏

发表于 | 更新于 | 分类于 | 阅读次数：

实验任务

小八同学最近开发了一款卡片收集的小游戏，在这个游戏中，小八同学布下了一个神奇的迷宫：

迷宫可以看成是一个二维的方格阵列，玩家初始不携带任何卡片，从左上角的入口处进入，右下角的出口走出。玩家每经过一个格子会获得或者失去一定数目的卡片，若玩家到了某一格需要支付卡片，但数目不足以支付的话，则清空其所携带的所有卡片，并允许其继续前行。最终的目的是保证用户从出口出来时尽量保留有更多的卡片。

现在规定玩家只能向右或者向下走，向下走每次只能走一格，但是如果向右的话，则每次可以走一格或者走到列数是当前所在列数数倍的格子，即如果当前格子是\((x,y)\)，则下一步可以是\((x+1,y)\)，\((x,y+1)\)或者\((x,y\times k)\)，其中 \(k>1\) 且为正整数。

现在请你计算玩家走出迷宫时所携带的最多的卡片数。

数据输入

第 1 行为两个正整数\(n\ m\)，其中 \(n\ (1\leq n\leq 20)\)，\(m\ (10\leq m\leq 1000)\)，分别表示行数和列数。接下来 \(n\) 行 \(m\) 列，表示迷宫的情况，数字范围为\(-1000\sim 1000\)。

数据输出

输出只有一行，表示玩家到达出口时剩余的最多卡片数。

输入示例 输出示例
3 8
9 10 10 10 10 -10 10 10
10 -11 -1 0 2 11 10 -20
-11 -11 10 11 2 10 -10 -10		 52

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<string.h>
#include<stdio.h>
const int maxn = 25;
const int maxm = 1005;
int dp[maxn][maxm], arr[maxn][maxm];

inline int max(int a, int b){ return a<b ? b : a; }

int main(){
  int i, j, k, n, m;
  scanf("%d%d", &n, &m);
  for (i = 1; i <= n; ++i){
    for (j = 1; j <= m; ++j){
      scanf("%d", &arr[i][j]);
    }
  }
  memset(dp, 0, sizeof(dp));
  dp[1][1] = max(0, arr[1][1]);
  for (i = 1; i <= n; ++i){
    for (j = 1; j <= m; ++j){
      if (i + 1 <= n) dp[i + 1][j] = max(dp[i + 1][j], dp[i][j] + arr[i + 1][j]);
      if (j + 1 <= m) dp[i][j + 1] = max(dp[i][j + 1], dp[i][j] + arr[i][j + 1]);
      for (k = 2*j; k <= m; k+=j){
        dp[i][k] = max(dp[i][k], dp[i][j] + arr[i][k]);
      }
    }
  }
  printf("%d\n", dp[n][m]);
  return 0;
}

设计思路与复杂度分析

填表法：设\(dp[i][j]\)表示从\((1,1)\)到达\((i,j)\)位置时能够获得的最多卡片数。则由题意描述，容易得到状态转移方程：\(dp[i][j]=max(dp[i][j],dp[i-1][j],dp[i][j-1],dp[i,j/fk])+a[i][j]\) （\(fk\)表示\(j\) 的因子，需要预处理出\(j\)的所有因子)。下图为当\((i,j)=(3,8)\)时的一个例子。

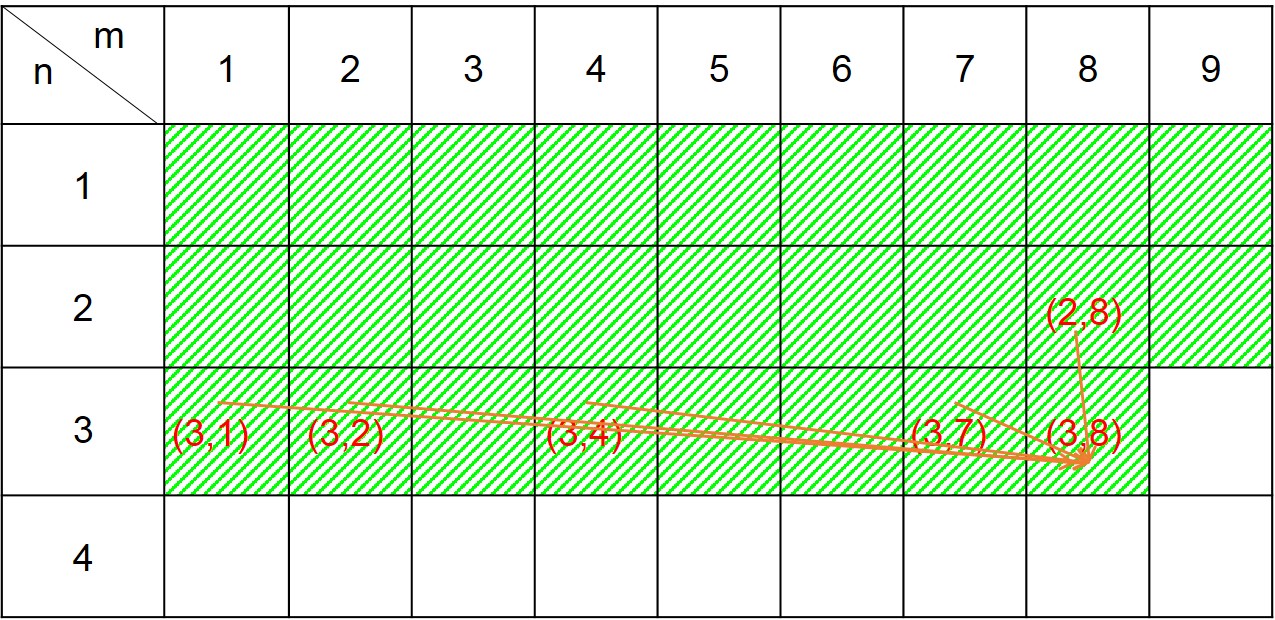
刷表法：现在假设我们已经得到从\((1,1)\)到达\((i,j)\) 这个位置的最优值\(dp[i][j]\)，我们利用它去更新下一步能够到达的位置。假设下一步为\((i',j')\)，则有状态转移方程\(dp[i'][j']=max(dp[i'][j'],dp[i][j]+a[i'][j'])\)。下图为当\((i,j)=(2,2)\) 时的例子。

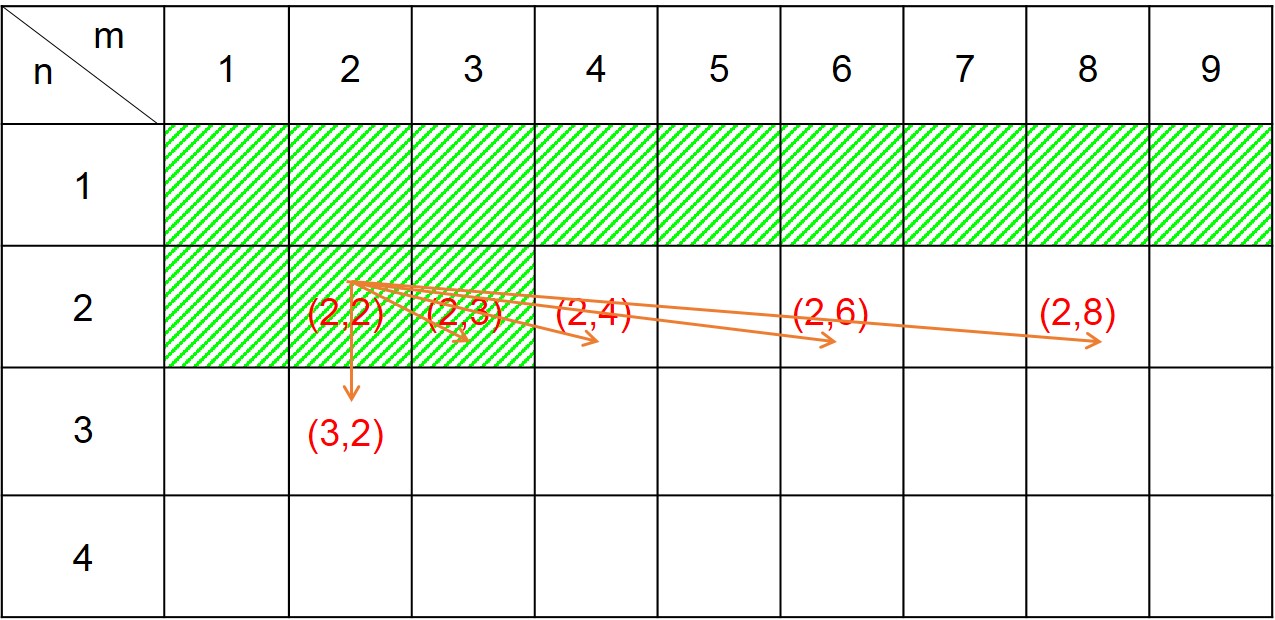
易知填表法思路直观但需要预处理出所有列的因子，而刷表法不需要预处理出因子。所以刷表法效率高于填表法。刷表法时间复杂度计算如下：

\[\begin{equation}\begin{split} T(n,m) &=n\times (m+m/2+m/3+m/4+...+m/m)\\\\ &=n\times m\times (1+1/2+1/3+...+1/m)\\\\ &=n\times m\times (ln(m)+C)\\\\ &=O(n\times m\times log(m)) \end{split}\end{equation}\]

0%